Coordination Game

View FREE Lessons!

Definition of Coordination Game:

A coordination game is a type of simultaneous game used in game theory when players benefit from coordinating their activities by making the same decisions. There are multiple Nash equilibria.

Detailed Explanation:

When two players have a common goal and can benefit from coordinating their actions, they are playing a coordination game. An example is when two drivers are traveling too fast on a narrow road and must immediately decide which way to swerve to avoid a collision. Their common goal is to prevent an accident. They must make independent and simultaneous decisions on which way to turn. If both drivers swerve to their right, then a collision is avoided. Likewise, if each swerves to the left, they prevent a collision. But if they swerve in opposite directions, they will collide. The two Nash equilibria are when both swerve right and when both swerve left.

The “stag hunt” is commonly used in game theory literature to illustrate a coordination game. Jean-Jacques Rousseau developed the hunt. In the stag hunt, two hunters, Dick and Derrick, have the choice of hunting a stag or rabbits. Teamwork is required to hunt a stag, while individuals can hunt rabbits. They are unaware of each other’s decisions when they enter the woods. Each hunter receives five points for killing a stag and two points for killing a rabbit. If one hunter chooses to hunt a stag, the other hunter could kill two rabbits and have a satisfaction of four. The resulting payoff table is presented below, with Derrick’s payoffs in purple and Dick’s in green.



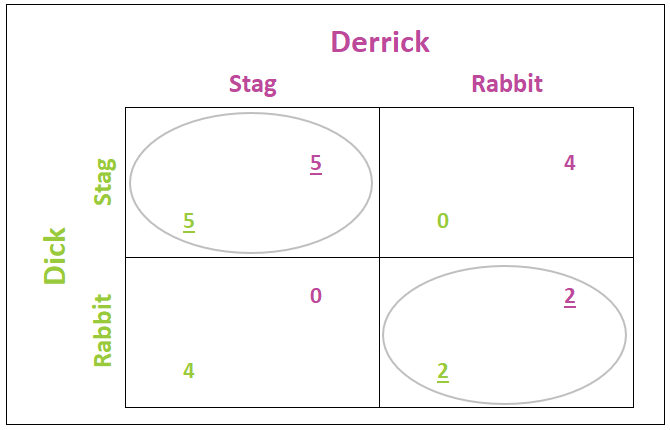
If Derrick believes Dick will hunt stag, then he maximizes his satisfaction by teaming with Dick to hunt stag, as shown on the first line of the payoff matrix. The underlined five in purple indicates that five is preferable to four. However, if Derrick believes Dick will choose to hunt rabbits, he would attain a higher score by also choosing to hunt rabbits because he prefers a score of two to zero - as illustrated in the second row of the table. Dick has the same set of decisions. If he believes Derrick will choose to hunt for a stag, he will consider the outcomes in the first column. His level of satisfaction is higher when he also decides to hunt stag because he prefers a payoff of five to four, which is shown by underlining the five in green. The second column contains the outcomes if Derrick chooses to hunt rabbits. In this case, Dick would also prefer hunting rabbits.

The two Nash equilibria are circled: one where both hunt stag and the other where both hunt rabbits. A Nash equilibrium results when no player has any incentive to change his strategy for personal gain – assuming each player’s decision remains unchanged after learning the other players’ decisions. It is impossible to determine the most probable decision, as it depends on the personalities of the hunters. If both are risk-takers, the stag, stag option is the most likely outcome. Economists refer to this decision as “payoff dominant.” Conversely, if both players are risk-averse, then the probable outcome is both choosing to hunt rabbits, which is the “risk dominant” strategy.


Image from iStock

Game theory can demonstrate the likelihood of a trade war without trust and verifiable agreements between two countries. Consider the possible escalation of a trade war between the United States and China. In 2019, American President Donald Trump and Chinese President Xi Jinping imposed tariffs on imported goods. While politicians often react to what other nations do, let’s consider a scenario where President Trump and President Xi impose tariffs simultaneously, without knowing what the other world leader will decide to do. 

A tariff is a tax on imported goods paid by the exporting companies. For example, if the United States charges a tariff on steel imported from China, the Chinese steel manufacturer pays the tariff to the US government. Most economists believe tariffs harm an economy by restricting trade. The quantity demanded for goods produced in the exporting country is reduced because the price increases in the importing country. The importing country is harmed because the price of the imported good or service is higher. Prices of domestic goods also increase, especially if they use materials supplied by foreign manufacturers. 

The payoff matrix displays both countries’ potential strategies and the payoffs associated with each outcome. One possibility is a full-scale trade war, where China and the United States impose tariffs on the other country’s goods. In this situation, each country suffers a drop in trade, higher prices, and the deterioration of their diplomatic relations with the other country. Assume each country’s payoff, in this case, equals -25 (for a $25 billion drop in GDP), shown in the upper left quadrant. 

If neither country imposes a tariff, then both countries receive a payoff of 75 (for a $75 billion increase in GDP), as seen in the bottom right quadrant. This high payoff is due to both countries being able to trade freely, thus benefiting from their comparative advantages while maintaining positive diplomatic relations.

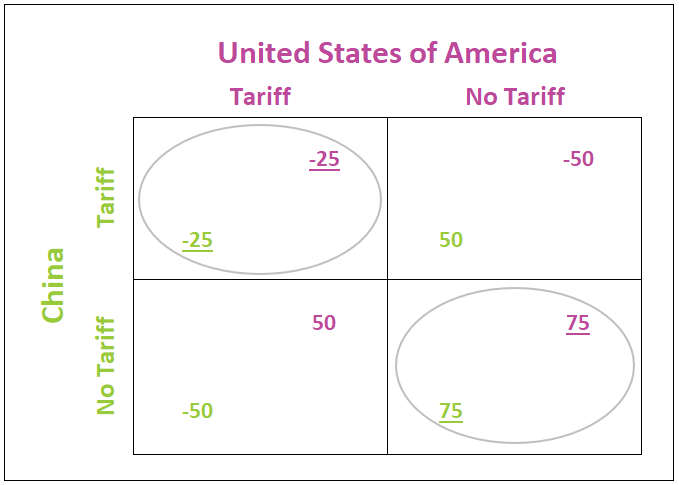
The remaining possibilities are that one country imposes a tariff, and the other does not retaliate. For example, suppose the United States imposes a tariff, and China does not retaliate. In that case, China’s payoff equals -50 because Chinese goods are now more expensive in the United States, resulting in a corresponding drop in the quantity demanded for Chinese goods in the United States. The United States payoff equals 50 because US companies sell more to US consumers who substitute US goods for Chinese goods. However, the payoff is less than 75 because US consumers pay higher prices for US and China-produced goods. In addition, US companies continue to export the same quantity of goods abroad without the tax. The bottom left quadrant represents this outcome. The upper right quadrant assumes the reverse would be true if China imposes a tariff and the US chooses not to respond.

This scenario has two Nash equilibria, each occurring when the countries make the same decision. If China believes the US will impose a tariff, its best outcome is to tax US imports, but if China thinks the US will not impose a tariff, its best strategy is also not to impose a tariff. It is never the best scenario for one country to refrain from imposing a tariff if it expects the other country to do so, making these options not NEOs. Economists refer to this as a coordination game because there are two Nash equilibria where both players play the same strategy, and neither player has a dominant strategy.

Dig Deeper With These Free Lessons:

Game Theory
Market Structures I – Perfect Competition and Monopoly
Market Structures II – Monopolistic Competition and Oligopoly
Comparative Advantage and Specialization