Tacit Collusion

View FREE Lessons!

Definition of Tacit Collusion:

Tacit collusion occurs when companies agree on a strategy without a formal written agreement. Price leadership is an example of tacit collusion.

Detailed Explanation:

Tacit collusion occurs when companies “agree” to collude without getting together to officially hammer out details. Is tacit collusion legal? Sometimes. If the senior managers get together privately to discuss the state of their industry and agree on a strategy to limit competition then the meeting is probably illegal, but it would be very difficult to prove if nothing is put in writing. Tacit collusion is frequently legal. Businesses can send signals. Press releases or public statements hinting at price increases provide a signal to competitors. For example, a high-ranking manager in a company may speak to the media or at a trade show. She may say that costs are rising, and a price increase may be necessary in the future. Her real audience is probably her competitors. The company may raise its price, and the other companies may follow.

Price leadership is common among oligopolies. Price leadership provides a way to increase prices without explicit collusion. One company takes on a leadership role in setting its price and the others normally follow. How are price leaders chosen? Usually, the dominant company sets an industry’s price. Less common is the barometric model, which gives the company with the best reputation at foreseeing future trends the pricing power. 

The challenge is getting all the companies to agree on how each party will price their goods or services. It may be relatively easy to reach an agreement between a few companies. The larger the number of companies, the more difficult it is to collude. Explicit collusion is usually illegal. Anti-trust laws prohibit discussing pricing or production quotas between competitors. This makes it more difficult to "enforce" tacit agreements because nothing is in writing and managers would deny reaching an agreement. 

Even when collusive agreements are legal, they don’t always form. Why? Companies have an incentive to cheat. Most often, the cheater wants to increase its sales and market share, so it reduces its price to less than the agreed-upon price. Competitors retaliate by lowering their price when their market share is threatened, initiating a price war. Price wars usually signify the end of a collusive agreement.

Game theory can be used to illustrate the low probability of maintaining high prices. Suppose there are only two restaurants in a small community, Bob’s Diner and Kathy’s Deli, and each is presently earning an economic profit of $30,000 annually. If they collude and price high they could each earn $50,000, but they have an incentive to cheat. Table 1 is a payoff matrix that can be used to predict the most likely outcome. Note that in this analysis, only the payoffs associated with the first year’s profits are considered. If Kathy and Bob can reach and honor a collusive agreement (explicit or tacit), they would split the higher profits evenly. In this case, they increase their profits from $30,000 to $50,000, as shown on the bottom right quadrant in Table 1.

Table 1


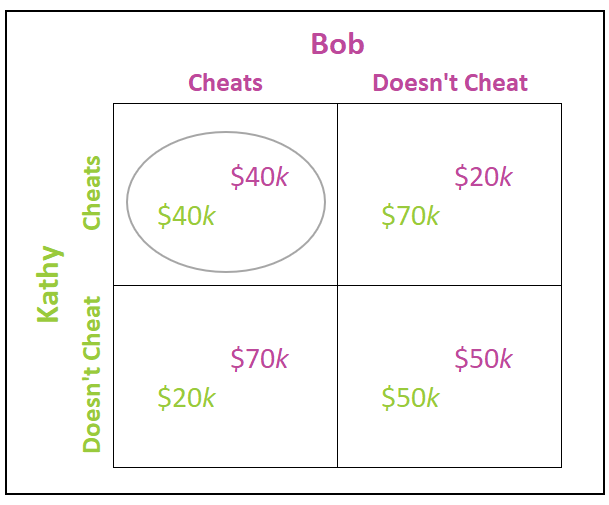
Let us examine Bob and Kathy’s incentive to cheat. Suppose Bob wants to increase his market share and lowers his prices to less than the agreed-upon prices. By charging lower prices, Bob reduces the total available profit from the maximum of $100,000 down to $90,000. But, because Bob’s prices are lower than Kathy’s, he attracts most of the customers. Kathy simultaneously chooses not to cheat. Bob earns $70,000 while Kathy’s profit falls to $20,000, as shown in the bottom left quadrant of the payoff matrix. Kathy suffers a loss by keeping the agreement. Of course, Kathy could just as likely be the “cheater”, in which case the situation would be reversed, with Kathy earning $70,000 and Bob's profits would fall to $20,000 because he honored the agreement. This scenario is shown in the upper right quadrant. Finally, assume Kathy and Bob both break the agreement. If both players cheat, both charge less than the agreed-upon prices. For simplicity, assume $80,000 is the total profit which they split evenly. Each earns an economic profit of $40,000, as seen in the upper left quadrant. 

Cheating is both Kathy and Bob’s dominant strategy, which means it is likely each restaurant owner would earn an economic profit of $40,000 that year. This outcome is circled in Table 1. Note that this is more than the $30,000 they would have earned had they not colluded. But consider the following years. Clearly, neither Bob nor Kathy can be trusted to keep the terms of their agreement, so both will likely lower their prices either in fear of what the other will do or to gain market share. Price reductions by one will be matched or exceeded by the other. In other words, a price war ensues. Prices could fall to a point where Kathy and Bob will earn zero economic profit. In other words, both Kathy and Bob will earn an economic profit of $40,000 over the course of two years – $40,000 from the year in which they both cheat and zero in the second year during the price war.

Table 2



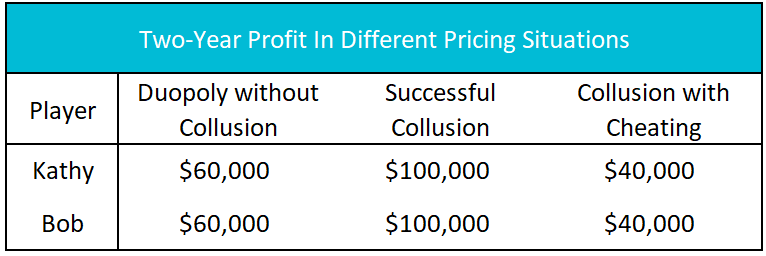
Table 2 summarizes Kathy and Bob’s possible pricing arrangements over two years. Not included is the possibility that one cheats while the other remains true to the agreement. This is highly unlikely because if one party cheated, the other would be forced to retaliate to protect his or her market share. The best two-year outcome for both Kathy and Bob is to successfully collude. Both would earn $100,000, or $50,000 per year. However, using game theory to solve the simultaneous game proves any collusive agreement is likely to eventually break down and result in a price war.

Most likely, Bob and Kathy would avoid a price war and choose to differentiate their restaurants. Perhaps one would choose to offer more of an Italian fare, while the other stresses traditional American. One could become a sport’s bar, while the other remains a family-style restaurant.

Dig Deeper With These Free Lessons:

Market Structures Part II – Monopolistic Competition and Oligopoly
Market Structures Part I – Perfect Competition and Monopoly
Game Theory